Transducers, gauges, sensors - Information portal © 2011 - 2025 Use of material is possible by placing an active link
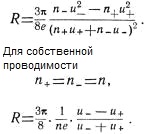
Effect of Hall
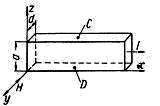
In 1879 the American physicist Hall opened the phenomenon which consists in the following. If through a homogeneous metallic or semiconductor plate to skip a current from left to right, along the axis of х, as it is shown on figs. 1, then equally potential lines will be straight lines, parallel to the rib of plate, to going along the axis of z, and between the symmetric located points C and D will exist to no difference of potentials. If after to place a plate in the magnetic field so that the last was directed along an axis at, i.e. was perpendicular to the steam-lines, then between points C and D arises up difference of potentials, the size of which is proportional to both the size of current of I and tension of magnetic-field of H. This phenomenon, getting the name of effect of Hall, can be explained as follows. Force operates on a locomotive in the magnetic field electric charge
F = eVHsin j
where е is a size of charge; V is his speed;
Н-напряженность of magnetic-field, and j is a corner between directions of V and Н.
If j = 90° (when the magnetic field is perpendicular to direction of locomotive charge), then force of F has a maximal value, equal еVН and directed athwart to directions of speed and magnetic-field.
It is known from the elementary course of mechanics, that if on a locomotive body force operates and directions of speed and force are mutually perpendicular here, then force veers only speed, not changing her size, and a self body moves on a circular trajectory with the radius of curvature of r. Obviously, what in examined case of motion of electric charge in the permanent magnetic field a charge will move on the circumference of radius of r, the walue of which can be found, if to take into account that centrifugal force of mV2/r is numeral equal to operating on a charge force of еVH, i.e. mV2/r = еVH, from where r = mV/eH
In a semiconductor or in a metal, placed in the magnetic field at passing of current, his formative electrons under influence of operating on them magnetic force will begin to deviate upwards or downward depending on directions of H and V. If electrons move from right to left, they will deviate upwards and to charge the supremum of plate negatively. Hereupon there will be the transversal electric field by tension in Е V/m and between points C and D will appear difference of potentials U:
U=Еа,
where and is a height of rib of plate (figs. 1).
русский / english
Home >> Magnetic field >> Effect of Hall
• Information about various converters and sensors of physical quantities, parameters of various physical processes is presented.
• Electrophysical properties and effects in various electrical materials.
• Theory, experimental results, practical application
Abludent up electrons will charge a supremum until the равновесное state which a transversal current will disappear at will not come. This state will come then, when electric force Her it will become to equal magnetic force of еVН i.e. еЕ = еVН. A current, current through a semiconductor plate, will be equal
I = nеVаd
where n is a concentration of transmitters of current.
Putting a value V, got from the last formula, will have
Е = IH/ nead
On the other hand, we found out that difference of potentials between points C and D is equal U = Еа. Putting his value instead of Е, will get final expression for
U = IH/ned
From this formula evidently, that the difference of potentials, arising up between two points of semiconductor, is proportional to both the current of I and tension of magnetic-field of Н. Shot of 1/ne for every this semiconductor, being at a the same temperature, is a permanent size, getting the name permanent Hall. More exact theory, taking into account participating in the current of electrons, possessing different speeds, gives for permanent Hall, usually designated through R, expression
R = 3π/8(1/ne) *
Thus, studying the effect of Hall in semiconductors, measuring the size of R, it is possible to determine the concentration of transmitters of n, and on a sign arising up between points C and D of difference of potentials is a mechanism of conductivity of semiconductors. For a p-type semiconductor, permanent Hall has a positive value, and for electronic - negative.
It is necessary to mean that by means of effect of Hall it is possible to determine the concentration of transmitters of current only in semiconductors, possessing some by one mechanism of conductivity - p-type or electronic. If a semiconductor has the mixed or own conductivity, then a passing in a semiconductor plate current is conditioned by motion of holes one-way and electrons in opposite. At the set direction of current and magnetic-field of rejection of holes and electrons coincide: and those, et al deviate or to the infimum of plate, or to overhead. Arising up between points C and D the difference of potentials of U will be determined in this case already by more difficult expression, where the concentrations of transmitters of current and their mobility enter. It is undifficult to understand from the cleanly physical considering, that a size and sign of U will depend on correlation of sizes of concentrations of holes and electrons and them mobility. In the separate special cases U can equal a zero.
For the semiconductors of the mixed type - permanent Hall determined by expression (here, U is the mobility of current carriers)
Literature: M. S. Sominskii. Semiconductors and their applications, 1956
Note:
* When using in the calculation system of units CGS Hall constant is equal to R = 3π/8(1/cne), where c=3⋅10^8 m/s - electrodynamic constant
See also:
Video. The Hall Sensor. Physical processes:

See also:
CONVERTERS, GAUGES, SENSORS
Information, news, advertising


