Transducers, gauges, sensors - Information portal © 2011 - 2025 Use of material is possible by placing an active link
Home >> Electricity, capacity, piezoelectricity. >>> Capacitive transducers, sensing elements, sensors
русский / english
• Information about various converters and sensors of physical quantities, parameters of various physical processes is presented.
• Electrophysical properties and effects in various electrical materials.
• Theory, experimental results, practical application

With the practical use of this method, two cylindrical or flat measuring electrodes are immersed in a controlled tank and the capacitance between them is determined, by the value of which, with a known ε2 controlled medium, the height of the filling level is calculated. Usually the scale of the indicating device is graduated in level units. The method is non-inertial, since the capacity changes simultaneously with the change in the filling level h2.
When measuring the thickness of the layers of insulating materials (films, fabrics, lacquer coating thickness, etc.), the test material is passed in the gap between the measuring capacitor plates. The advantage of this method is its non-contact. The method makes it possible to determine the air content in foams and similar materials at known sample sizes and dielectric permittivity of the material itself.
Since, for example, water in comparison with air has a much greater dielectric constant, with the help of this dependence it is possible to determine the moisture content of various insulating materials. In comparative measurements, it is important that the dielectric permittivity of the test materials differ slightly. A significant difference in the dielectric permittivity of air and many liquid and solid materials, especially water, allows the capacitive method to measure the position of the level and the state of filling the vessels, as well as the thickness of the ice. In this case, two parallel connected tanks are considered, since ε1 = 1, then
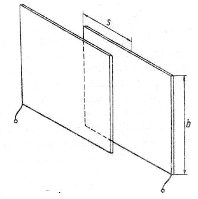
Fig. 3. Flat capacitor with variable plate overlap
In the capacitor capacitance equation, the value S is the area of mutual overlap of the plates. The displacement of both plates relative to each other by the value of s can change the area of their overlap, and for rectangular plates the dependence S = bs is linear (Fig. 3). Since the value of S is in the numerator of the capacitance equation of the capacitor C, C is linearly dependent on s. The use of plates of different shapes allows to obtain quadratic, logarithmic, etc. dependences. Variable capacitance capacitor consisting of round rotary plates, is applicable for measuring the angle of rotation.
Sensitive elements with variable dielectric constant of the gap
Capacitive sensing elements, based on the measurement of changes ε, used mainly to determine the composition of substances (with full filling of the gap controlled environment) and to measure the level of the changing filling of the gap. The level can be changed both along and across the plates. When controlling the composition of solids (e.g. sand, dust, gravel, etc.), as well as liquids (vapors, gases or wet materials), they can be placed inside a flat or cylindrical condenser. For a fully filled measuring capacitor, there is a proportional dependence:
Like the inductive sensing element with transverse armature movement and dual windings, the differential principle and in this case, along with the doubling of the sensitivity provides the expansion of the linear range. At Δd /d = 0,1, the nonlinearity of the characteristic of such a capacitor is 1 %.
Sensing element with variable plate area
Only at small relative changes of the gap Δd/d the dependence between ΔС/С and Δd/d is practically linear. When Δd /d = 0,1 non-linearity is 10%, when Δd /d = 0,01 to ~ 1 %. To ensure linearity in a wide range, a differential capacitor is used (Fig. 2). When moving the middle plate at a distance Δd, with the appropriate switching circuit (bridge circuit), the capacitance change is equal to
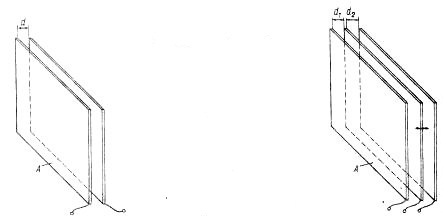
When changing the gap d between the plates (Fig. 1) the Δd value of the capacitance of the capacitor is determined by the equation
Fig. 1. Flat capacitor with variable gap
Fig. 2. Differential capacitor; middle plate can move in transverse direction
Capacitive transducers, sensing elements, sensors
The capacitance of a flat capacitor without taking into account the edge effect is determined by the equation С = ε0εS/d, where ε0 = 8,85⋅10∧12 А⋅с/(В⋅м) - the dielectric constant; ε - the relative permittivity of the medium between the capacitor plates; S - the area of the plates; d - the distance between them. The capacitance of the capacitor varies with the change in the area of the plates, the distance between them (gap) and the permittivity of the material.
Sensing elements with variable clearance
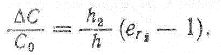
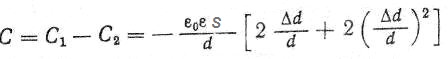
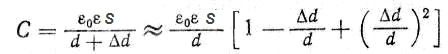
See also:
CONVERTERS, GAUGES, SENSORS
Information, news, advertising


