Главная >> Емкостные преобразователи, чувствительные элементы, датчики
Преобразователи, датчики, сенсоры - Информационный портал © 2011 - 2025 Использование материалов сайта возможно при размещении активной ссылки
русский / english
Емкостные преобразователи, чувствительные элементы, датчики
Емкость плоского конденсатора без учета краевого эффекта определяется уравнением С = ε0εS/d, где ε0 = 8,85⋅10∧12 А⋅с/(В⋅м) - диэлектрическая постоянная; ε - относительная диэлектрическая проницаемость среды, находящейся между пластинами конденсатора; S - площадь пластин; d - расстояние между ними. Емкость конденсатора изменяется при изменении площади пластин, расстояния между ними (зазора) и диэлектрической проницаемости материала.
Емкостные чувствительные элементы с изменяющимся зазором
• Представлена информация о различных преобразователях и датчиках физических величин, параметров различных физических процессов.
• Электрофизические свойства и эффекты в различных электротехнических материалах.
• Теория, экспериментальые результаты, практическое применение

Подобно индуктивному чувствительному элементу с поперечным перемещением якоря и сдвоенными обмотками дифференциальный принцип и в этом случае наряду с удвоением чувствительности обеспечивает расширение линейного диапазона. При Δd /d = 0,1 нелинейность характеристики такого конденсатора составляет 1 %.
Чувствительный элемент с изменяющейся площадью пластин
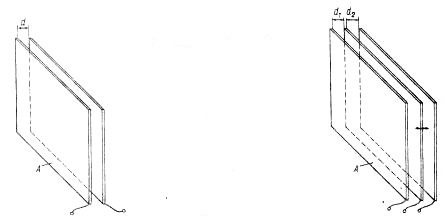
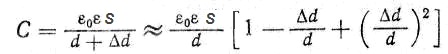
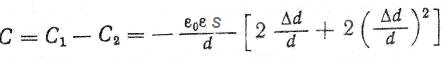
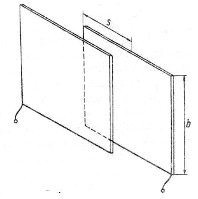
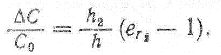
Рис. 1. Плоский конденсатор с изменяющимся зазором
Рис. 2. Дифференциальный конденсатор; средняя пластина может перемещаться в поперечном направлении
При изменении зазора d между пластинами (рис. 1) на величину Δd емкость конденсатора определяется уравнением
Только при малых относительных изменениях зазора Δd/d зависимость между ΔС/С и Δd/d практически линейна. При Δd /d = 0,1 нелинейность составляет 10%, при Δd /d = 0,01 ~ 1 %. Для обеспечения линейности в широком диапазоне применяют дифференциальный конденсатор (рис. 2). При перемещении средней пластины на расстояние Δd, при соответствующей схеме включения (мостовой схеме), изменение емкости равно
Рис. 3. Плоский конденсатор с изменяющимся перекрытием пластин
В уравнении емкости конденсатора величина S представляет собой площадь взаимного перекрытия пластин. Смещением обеих пластин относительно друг друга на величину s можно изменить площадь их перекрытия, причем для пластин прямоугольной формы зависимость S = bs линейна (рис. 3). Поскольку величина S находится в числителе уравнения емкости конденсатора С, то С линейно зависит от s. Использование пластин различной формы позволяет получить квадратичные, логарифмические и т. п. зависимости. Конденсатор переменной емкости, состоящий из круглых поворотных пластин, применим для измерения угла поворота.
Емкостные чувствительные элементы с изменяемой диэлектрической проницаемостью зазора
Емкостные чувствительные элементы, основанные на измерении изменения ε, применяют главным образом для определения состава веществ (при полном заполнении зазора контролируемой средой) и для измерения уровня при изменяющемся заполнении зазора. Уровень можно изменять как вдоль, так и поперек пластин. При контроле состава твердых веществ (например, песка, пыли, гравия и т. п.), а также жидкостей (паров, газов или влажных материалов) их можно помещать внутри плоского или цилиндрического конденсатора. Для полностью заполненного измерительного конденсатора существует пропорциональная зависимость:
Так как, например, вода по сравнению с воздухом обладает значительно большей диэлектрической проницаемостью, то с помощью указанной зависимости можно определять влагосодержание различных изоляционных материалов. При сравнительных измерениях важно, чтобы диэлектрические проницаемости исследуемых материалов различались незначительно. Существенное различие диэлектрических проницаемостей воздуха и многих жидких и твердых материалов, прежде всего воды, позволяет измерять емкостным методом положение уровня и состояние заполнения сосудов, а также толщину льда. В этом случае рассматривают две параллельно соединенные емкости, причем так как ε1 = 1, то
При практическом использовании данного метода в контролируемый резервуар погружают два цилиндрических или плоских измерительных электрода и определяют емкость между ними, по значению которой при известном ε2 контролируемой среды рассчитывают высоту уровня заполнения. Обычно шкала показывающего прибора градуируется в единицах уровня. Метод безынерционен, так как емкость изменяется одновременно с изменением уровня заполнения h2.
При измерении толщины слоев электроизоляционных материалов (пленок, тканей, толщины лаковых покрытий и т. п.) исследуемый материал пропускают в зазоре между измерительными обкладками конденсатора. Достоинством этого метода является его бесконтактность. Метод позволяет определять содержание воздуха в пенопластах и подобных им материалах при известных размерах образцов и значениях диэлектрической проницаемости самого, материала.
Смотрите также:
ПРЕОБРАЗОВАТЕЛИ, ДАТЧИКИ, СЕНСОРЫ
Информация, новости, реклама


