Преобразователи, датчики, сенсоры - Информационный портал © 2011 - 2025 Использование материалов сайта возможно при размещении активной ссылки
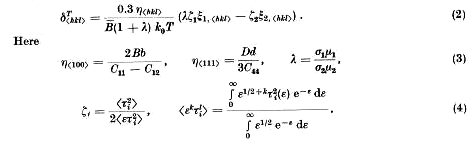
Главная >> Литература >> Пьезо Холл эффект в р-германии
русский / english
• Представлена информация о различных преобразователях и датчиках физических величин, параметров различных физических процессов.
• Электрофизические свойства и эффекты в различных электротехнических материалах.
• Теория, экспериментальые результаты, практическое применение
phys. stat. sol. (b) 100, 309 (1980)
Subject classification: 12.2 and 14.3; 22.1.1
Institute of Semiconductors, Academy of Sciences of the Ukrainian SSR, Kiev1)
Пьезо Холл эффект в р-германии
Н. Т. Горбачук, В. В. Митин, Ю. А. Тхорик, Ю. М. Шварц
В интервале температур от 77 до 300 К в образцах р-Gе с малым (ρзоок = 0,02 Ом⋅см) и большим (ρзоок = 16 Ом⋅см) сопротивлением исследован пьезо Холл эффект для случая, когда ток i и одноосное давление х параллельны осям <100> и <111> кристалла. При трактовке экспериментальных результатов учтена анизотропия закона дисперсии легких и тяжелых дырок, что позволило объяснить различие температурных зависимостей коэффициентов пьезосопротивления для образцов с малым и большим ρ, а также ориентационную зависимость эффекта. Получены значения констант деформационного потенциала b и d которые в зависимости от известных в литературе значений зонных констант А, В и С изменяются в пределах b = - (2,2 до 2,6) еВ, d = - (4,4 до 5,1) еВ, что существенно отличается от b и d полученных по тем же экспериментальным данным без учета анизотропии закона дисперсии.
1. Введение и формулы для расчета
Пьезо Холл эффект в р-Ge был исследован в работах [1, 2]. Тем не менее, анизотропия закона дисперсии (АЗД) не была принята во внимание в расчетах и, следовательно, в интерпретации результатов эксперимента. Принимая во внимание АЗД при расчете пьезосопротивления видно достаточное влияние на результаты расчета (см., например, [3]). Следовательно, представляет интерес рассмотреть это влияние и на пьезо Холл эффект тоже.
Зависимость коэффициента Холла от величины одноосного X напряжения определяется выражением
(1)
где R0(μ1σ1 + μ2σ2)/[c(σ1 + σ2)] ; μi; σi - Холловская подвижность и проводимость легких (i = 1) и тяжелые (i = 2) дырок, соответственно, δ<hkl> + 1/2π<hkl> - коэффициент пьезо Холл эффекта, π<hkl> - коэффициент продольного пьезосопротивления, δ<hkl> = δ0<hkl> + δT<hkl> , δ0<hkl> - не зависящая от температуры и δT<hkl> зависящая от температуры компоненты δ<hkl>.
Для интерпретации результатов эксперимента только δT<hkl> используются. Выражения для δT<hkl> могут быть легко получены в соответствии с [4]
ε - энергия дырок в k0T единицах, B = √ B^2 + C^2/5, B, D, C постоянные валентной зоны [4]. В (2) только те параметры ξi,<hkl>, которые зависят от АЗД. Их аналитическое выражение написано в приложении, потому что это обременительно. Как следует из приложения, пренебрежение АЗД дает ξi,<hkl> = 1, а принимая это обстоятельство получаем
отклонение ξi,<hkl> от единицы.
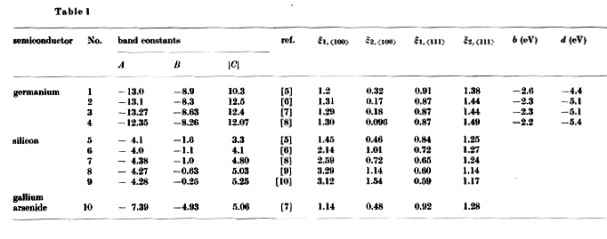
Мы подсчитали, ξi,<hkl> по формулам Приложения и различных наборов констант A, B, C, которые известны [5 - 10] для р-Ge, Si р-и п-GaAs. Результаты приведены в таблице 1. Как видно из таблицы, параметры ξi,<hkl> для Ge незначительно отличаться от одной к другой в связи с небольшим отличием различных наборов констант A, B и C. Совершенно другая ситуация имеет место в Si, для которых разброс значений A, B, C и велик.
2. Результаты экспериментов и их сравнение с расчетными данными
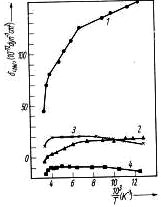
Были исследованы образцы р-Ge сопротивлением ρ300 K = 16 Ом⋅см и ρ300 K = 0,02 Ом⋅см и размерами 0,7 х 0,7 х 8 мм ^ 3 . Измерения проведены вдоль <100> или <111>. Зависимость R и ρ от X измерялась при малых нагрузках (в области линейной зависимости этих значений от напряжения) в диапазоне температур от 77 до 300 K для i | | х | | <100> и i | | х | | <111> (i это вектор тока). π<hkl> = (ρx - ρ0)/ρ0X и δ<hkl> +1/2 π<hkl> = (Rx - R0)/R0X (т.е. экспериментальная зависимость δ<hkl> от температуры) были определены (см. рис . 1). Как видно из рис. 1, в относительно чистом полупроводнике (кривые 1 и 2)
Рис. 1. Температурная зависимость δ<100> ((1) и (3)) and δ<111> ((2) и (4)) в p-Ge. (1) и(2) ρ300 K = 16 Ом⋅см, (3) и (4) ρ300 K = 0.02 Ом⋅см
δ<100> и δ<111> положительны и увеличиваются с ростом 1 / T. Это указывает на преобладающий вклад легких дырок в δ<hkl> - см. (2). Предположим, λ = 2,8, ζi = 1 (это правильно, если рассеяние на акустических фононах является преобладающим), C44 = 6,67 х 10 ^ 11 дин на сантиметр ^ 2, C11 - C12 = 8,02 X 10 ^ 11 дин/см2 [11 ]. После этого мы получим значения констант деформационного потенциала (см. таблицу 1) Из сравнения теоретических и экспериментальных наклонов δ<hkl>(1 / T) для области, где δ<hkl> линейно зависит от 1 / T.
Пренебрегая АЗД ( ζi,<hkl> = 1) b и d получим одинаковыми для всех множеств групп параметров, перечисленных в таблице 1 (b ≈ -4,4 эВ, d ≈ -2,8 эВ). Эти значения значительно отличаются от b и d полученных нами с учетом из АЗД. Кроме того, этот результат (| b |> | d |) находится в противоречии с литературными данными [12]. Поэтому, необходимо принимать во внимание АЗД в интерпретации результатов эксперимента. Особенно следует отметить, что в отличие от случая i | | х | | <100>, для которых λξ1,<100> >> ξ2,<100> и вклад легких дырок является основным, значение ξ2,<111> ,близко к λξ1,<111> для i || x || <100>. Вот почему разница λξ1,<111> — ξ2,<111> очень чувствительна к выбору λ значения. В частности, если λ меньше, чем 1,52; 1,66; 1,71, и 1,66 для первого, второго, третьего и четвертого набора констант, соответственно, эта разница всегда имеет другой знак.
Наклон δ<hkl>(1 / T) для сильно легированного полупроводника (СЛП) практически равен нулю при температуре более 120 K (кривые 3, 4). Это вызвано уменьшением ζi и λ (для рассеяния на ионизированных примесях ζi = 1/9, λ ≤ 0.36). Несмотря на малые наклоны кривых 3 и 4, следует отметить, что они имеют разные знаки. Это может быть объяснено преобладают вклады тяжелых дырок в δ<111> и легких дырок в δ<100> для λ≤ 1 (см. (2)). Наклон кривых δ<hkl>(1 / T) изменяется в образце с ρ = 0,02 Ом⋅см, если T <120 К. Это связано с переходом на другой механизм проводимости. В этом диапазоне температур ρ имеет максимум и снижение ρ с понижением температуры указывает на вклад прыжковой проводимости [13].
3. Заключение
Сравнивая значения b и d, полученные с учетом АЗД и без него, мы приходим к следующему выводу.
Необходимо учитывать АЗД в интерпретации пьезо Холл эффекта в р-Ge (в частности, в экспериментальном определении констант деформационного потенциала). Это обстоятельство позволяет объяснить экспериментально наблюдаемые особенности пьезо Холл эффекта в р-Се и получить достаточную точность оценки констант деформационного потенциала b и d.
Точность определения констант деформационного потенциала ограничена точностью, с которой известны группа параметров A, B, C. В Si, где разброс значений A, B, C большой, соответственно разброс значений ξi,<hkl> тоже большой. Это создает трудности для определения b и d.
Подтверждение
Авторы выражают благодарность А. Ю.Тхорику за выполнение численных расчетов
Ссылки
[1] M. Inoue and M.Ikeda, J. Phys. Soc. Japan 20, 1542 (1965).
[2] Г. Е. Пикус, Г. Л. Бир, ФТТ. 1, 1,828 (1959).
[3] Л. Бир, А. И. Блум, В. В.Илисавский. Proc. VII. Internat. Conf. Phys. Semicond., Paris 1964 (p. 529).
[4] Г.Л. Бир, Г.Е.Пикус . Симметрия и деформационные эффекты в полупроводниках, Наука, Москва, 1972 г..
[5] G. DRESSELHAUS, A. F. KIP, and C. KITTEL, Phys. Rev. 98, 368 (1955).
[6] B. LAX and J. MAVROIDES, Solid State Phys. 11, 261 (1960).
[7] И.М.Цидильковский. Зонная структура полупроводников. Наука, Москва 1978 год.
[8] F. POLLAK and M. CARDONA, Phys. Rev. 142, 530 (1.966).
[9] I. BALSLEV and P. LAWAETZ, Phys. Letters 19, 6 (1965).
[10] J. HENSEL and G. FEHER, Phys. Rev. 129, 1041 (1963).
[11] H. J. Mc SKIMIN and P. ANDREATCH, J. appl. Phys. 35, 3312 (1964).
[12] П. И. Баранский, В. П. Клочков, И.В.Потыкевич. Полупроводниковая электроника. Наукова думка, Киев 1975 (стр. 6).
[13] Б.И.Шкловский, А.Л.Эфрос. Электронные свойства легированных полупроводников, Наука, Москва 1979 (стр. 109).
(Поступило в феврале 1980 г.)

Смотрите также:
ПРЕОБРАЗОВАТЕЛИ, ДАТЧИКИ, СЕНСОРЫ
Информация, новости, реклама


