Общие основы работы измерительных преобразователей температуры - полупроводниковых терморезисторов
Описаны физические основы работы терморезистора. Полупроводниковый терморезистор, методика градуировки.
Терморезистором называют устройство, состоящее из проводника, электрическое сопротивление которого зависит от температуры и до которого подсоединены электрические выводы. Широкое применение находят полупроводниковые терморезисторы. В этом случае в качестве проводника электрического тока служит полупроводник в виде пленки на изолирующей подложке или в объемном исполнении. Чаще всего применяют такие полупроводники: Ge, GaAs, Si. Общие размеры терморезисторов могут быть менее 1 мм^3, электрическое сопротивление от нескольких Ом до 100 кОм, токи питания, как правило, 10 - 100мкА, чувствительность от 5 %/К в области комнатной температуры до 100 %/К в области криогенных температур, инерционность может достигать нескольких десятков миллисекунд.
Полупроводниковые терморезисторы широко применяются для измерения и контроля температуры в широком диапазоне, но, как правило, не выше 200 °С, так как при высокой температуре наступает собственная проводимость и температурная зависимость сопротивления резко падает, становится не монотонной, не стабильной. В широком диапазоне температур зависимость сопротивления полупроводника от температуры R(T) имеет сложный характер и зависит от типа легирующей примеси и уровня легирования. Поэтому невозможно выразить зависимость R(T) простой формулой, которая бы позволила выполнить градуирование с высокой точностью. Как правило, весь интервал температуры разбивают на отдельные участки, на которых зависимость R(T) описывается своей интерполяционной формулой.
Методику градуировки можно рассмотреть на следующем примере. В области комнатной температуры зависимость R(T) для полупроводниковых терморезисторов можно выразить:
R=Ro * e ^ B/T ( 1 )
Для градуирования терморезистора (получения таблиц зависимости электрического сопротивления от температуры) преобразуем формулу (1):
lnR = lnRo + B(1 /T ) ( 2 )
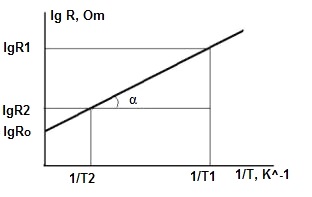
Полученное выражение (2) является уравнением прямой в координатах 1/T и LnR.
LnRо - величина логарифма сопротивления когда Т стремится к бесконечности . Коэффициент В равен тангенсу угла α наклона прямой к оси 1/Т. Если при двух фиксированных температурах Т1 и Т2 измерять сопротивления терморезистора R1 и R2 соответственно, то можно построить зависимость LnR(1/T) по двум точкам:
Главная >> Температура. Термоэлектричество. Основы работы терморезисторов
Преобразователи, датчики, сенсоры - Информационный портал © 2011 - 2025 Использование материалов сайта возможно при размещении активной ссылки
русский / english
Основы работы терморезисторов
Терморезисторы. Принцип работы
Платиновые и медные термосопротивления
Экспериментальные низкотемпературные терморезисторы
Низкотемпературные (криогенные) термометры (терморезисторы) и термопары.
Температура, термоэлектричество
• Представлена информация о различных преобразователях и датчиках физических величин, параметров различных физических процессов.
• Электрофизические свойства и эффекты в различных электротехнических материалах.
• Теория, экспериментальые результаты, практическое применение
Используя формулу (2) и полученный график можно находить для любого значения R из интервала от R1 до R2 соответствующее ему значение температуры (составить градуировочные таблицы).
Для точных измерений температуры градуировку терморезистора проводят в специализированных лабораториях с применением соответствующих аппроксимирующих формул для нужного диапазона температур, компьютерной обработки данных и др. В широком диапазоне температур температурная зависимость сопротивления полупроводникового терморезистора имеет достаточно сложный характер.

Смотрите также:
ПРЕОБРАЗОВАТЕЛИ, ДАТЧИКИ, СЕНСОРЫ
Информация, новости, реклама


