где , G - модуль сдвига связующего, Е - модуль упругости чувствительного элемента (образца), Q - площадь поперечного сечения образца, , h - толщина образца, hс - толщина связующего, l - длина образца.
Подставляя параметры наших условий измерения (для hс = 0,15 мм) получим kпер = 0,68. С учетом коэффициента передачи и расчета истинной деформации εо = εб x kпер в исследуемой пленке получим действительные величины коэффициентов тензочувствительности пленок kII = -40,1 и k⊥ = -3,8.
При измерении тензочувствительности методом прямого нагружения образец консольно закреплялся, и прикладывалась изгибающая нагрузка. Погрешность измерения коэффициентов данным методом не превышала 4%. При комнатной температуре получены следующие значения: πII = -24,9 и π⊥ = -2,4.
Если учесть упругие свойства кремния для используемой нами кристаллографической ориентации образцов и пересчитать полученные с помощью балки коэффициенты тензочувствительностит k в коэффициенты пьезосопротивления π (учитывая соотношение σ =Eε, где Е - модуль упругости, ε - относительная деформация), то получим, что расхождение в величинах π, измеренных разными способами, не превышает 6%. На наш взгляд, это говорит о хорошей точности формулы для kпер /8/ и необходимости учета коэффициента, особенно при размерах исследуемых образцов, превышающих толщину связующего. Следует отметить, что важное значение имеет корректность в определении величин hс и G формулы.
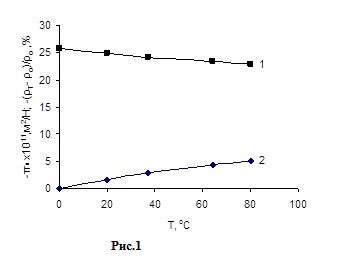
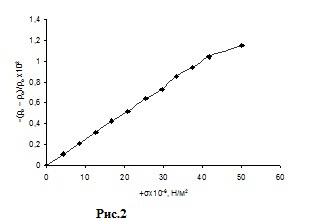
На рис. 1 приведены результаты измерения температурной зависимости π и ρ, а на рис. 2 показана зависимость ρ от продольных механических напряжений. Температурная зависимость удельного сопротивления равна 0,08 %/К, а тензочувствительности 0,15 %/К.
По сравнению с объемным кремнием и диффузионными слоями такого же уровня легирования /1, 3, 6/ соответствующие коэффициенты пьезосопротивления исследованных нами пленок близки к ним по величине, но температурная зависимость параметров ниже у пленок, легированных ионной имплантацией. Отличие может быть обусловлено поликристалличностью и более однородным легированием.
Заключение
Таким образом, исследования показали, что ионно-легированные поликристаллические слои кремния при сравнимой с другими видами кремния тензочувствительности обладают меньшей температурной зависимостью параметров. При исследовании тензочувствительности с помощью балки необходимо учитывать коэффициент передачи деформации образцу. В дальнейшем мы планируем провести исследования для различных уровней легирования, типов проводимости, кристаллографической ориентации.
СПИСОК ЛИТЕРАТУРЫ
1. Ваганов В.И. Интегральные тензопреобразователи. -М.: Энергоатомиздат, 1983. - 136 с.
2. Терстон Р. Применение полупроводниковых преобразователей для измерения деформаций, ускорений и смещений. -В кн.: Физическая акустика/ Под ред. У. Мэзона, т.1, часть Б -Методы и приборы ультразвуковых исследований. Пер. с англ. - М.: Мир, 1967, с.187-209.
3. Зеегер К. Физика полупроводников. Пер. с англ. под ред. Ю.К. Пожелы. -М.: Мир, 1977, с. 615.
4. Smith C.S. Phys. Rev., 1954, 94, c. 42.
5. Smith C.S. Piezoresistance effect in germanium and silicon. - Phys. Rev. 1954, v. 94, 1, p. 42-49.
6. Tufte O.N., Stelzer E.L. Piezoresistive properties of silicon diffused lauers.- J. Appl. Phys., 1963, v. 34, 9, p. 313-318.
7. Fouretier G. La Dynamometrie de Precision // Analyse des Contraintes. - 1957, v. 11, 9-10, p. 19-27.
8. Клокова Н.П. Тензорезисторы: Теория, методики расчета, разработки. - М.: Машиностроение, 1990. -224 с.
Источник: Горбачук Н.Т., Диденко П.И. Поверхность, 2006, 4, с.104-106.
Преобразователи, датчики, сенсоры - Информационный портал © 2011 - 2025 Использование материалов сайта возможно при размещении активной ссылки
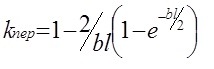
русский / english
Главная >> Публикации >> ИССЛЕДОВАНИЕ НЕКОТОРЫХ ЭЛЕКТРОФИЗИЧЕСКИХ СВОЙСТВ ПЛЕНОК n- Si, ЛЕГИРОВАННЫХ ИОННОЙ ИМПЛАНТАЦИЕЙ
• Представлена информация о различных преобразователях и датчиках физических величин, параметров различных физических процессов.
• Электрофизические свойства и эффекты в различных электротехнических материалах.
• Теория, экспериментальые результаты, практическое применение

ИССЛЕДОВАНИЕ НЕКОТОРЫХ ЭЛЕКТРОФИЗИЧЕСКИХ СВОЙСТВ ПЛЕНОК n- Si, ЛЕГИРОВАННЫХ ИОННОЙ ИМПЛАНТАЦИЕЙ
Введение
Электрофизические свойства полупроводников могут зависеть не только от типа легирующей примеси и концентрации, но и от способа легирования, который приводит к тому или иному распределению примеси в пространстве и другим сопутствующим технологии эффектам, в определенной степени влияющим на параметры. Применяемый на практике кремний условно разделяют на три класса: равномерно легированный, диффузионный и ионно-имплантированный /1/. Литературные данные свидетельствуют о том, что наименее исследованы электрофизические свойства ионно-имплантированного кремния.
Кремний находит очень широкое применение в тензометрии и авторов, в основном, интересовали тензочувствительность (пьезорезистивный эффект), удельное сопротивление и их температурная зависимость в ионно-имплантированных слоях кремния.
Теоретический анализ
Для общего случая, когда направление механического напряжения σ и плотности тока j составляют произвольный угол, пьезорезистивный эффект в полупроводниках с кубической решеткой теоретически описывается с помощью пьезорезистивных πij или эласторезистивных mij коэффициентов, которые являются тензорами четвертого ранга /1, 2/. Эти коэффициенты связаны между собой через коэффициенты податливости и модули упругости. Для кристаллов того класса симметрии, к которому принадлежит кремний, в системе кристаллографических осей для описания пьезорезистивного эффекта достаточно знать три коэффициента: π11, π12 и π44, которые иногда называют главными пьезорезистивными коэффициентами. Главные пьезорезистивные коэффициенты зависят от многих факторов: от материала, типа проводимости, удельного сопротивления, уровня легирования, температуры, величины механической деформации (напряжения).
В /3,4/, например, приведены известные различные комбинации коэффициентов пьезосопротивления для направлений механических напряжений и плотности тока, совпадающих с определенными кристаллографическими осями.
Все три главных коэффициента пьезосопротивления могут быть определены путем трех измерений в различных направлениях /3, 4/. Полный тензор пьезосопротивления πijkl определяется следующим образом:
где σkl - тензор напряжения, Δρij - тензор удельного сопротивления. Известно, что тензор напряжения является симметричным тензором и имеет шесть независимых компонент. То же самое справедливо и для тензора удельного сопротивления.
С учетом сказанного в шестимерном пространстве можно получить:
Для объе n-Si с равномерным легированием и ρ = 11,7 Ом·см в работе /5/ получены результаты: π11 = -102,2, π12 = 53,7, π44 = -13,6.
В слоях кремния с диффузионным легированием пьезорезистивные коэффициенты определяются концентрацией примеси на поверхности слоя Nп /6/ и практически не зависят от закона распределения примеси. Из полученных в этой же работе результатов видно, что для n-Si коэффициент π11 при комнатной температуре изменяется от 17·10^-11 м2/Н (Nп =1x10^21 см-3) до 88x10^-11 м2/Н (Nп = 1,8x10^18 см-3). Заметная температурная зависимость π11 начинается с Nп = 9·10^19 см-3 (примерно 0,1 %/К).
Следует отметить, что в связи с особенностями зонной структуры n-Si для не очень высокой степени легирования кремния справедливы допущения /5/:
π44 ≅ 0; π11 ≅ -2 π12
По мере увеличения концентрации примеси возникает нарушение этих допущений, что необходимо учитывать. Для диффузионных слоев нарушения происходят при Nп ≥ 5x10^19 см-3 /1, 6/.
Экспериментальная часть
Нами исследованы легированные ионной имплантацией фосфора тонкие поликристаллические пленки n-кремния на плоскости (100) монокристаллического кремния с изолирующим слоем SiO2. Такие структуры могут быть более технологичны при использовании планарных технологий изготовления измерительных преобразователей.
Экспериментально измерены удельное сопротивление ρ, коэффициенты продольной kII = ΔρII/ρII·εII (где ΔρII - изменение удельного сопротивления вдоль направления деформации εII), и поперечной k⊥ = Δρ⊥/ρ⊥·εII (где Δρ⊥ - изменение удельного сопротивления перпендикулярно направлению деформации εII) тензочувствительности, коэффициенты пьезосопротивления πII = (π11 + π12 + π44)/ 2 и π⊥ = (π11 + π12 - π44)/ 2, температурная и деформационная зависимости указанных величин.
Пленки получены на плоскости (100) кремния. Толщина пленок 0,6 мкм, концентрация легирующей примеси 5x10^18 см-3. Удельное сопротивление 0,013 Ом см. Измерения проведены на образцах размерами 8 x 0,6 x 0,4 мм с пленкой на поверхности.
Измерение коэффициентов пьезосопротивления проводилось как с помощью консольной стальной балки равного сопротивления изгибу, так и путем непосредственного нагружения образцов. При измерениях с помощью балки и использовании величины деформации, рассчитанной по известной формуле
εб = hδ / lб^2
(где h - толщина балки, lб - длина балки, δ - перемещение свободного конца балки) были получены значения коэффициентов тензочувствительности бkII (ε II <110>; J II <110>) и бk⊥ (ε II <110>; J ⊥ <110>) -27,3 и -2,8 соответственно. Однако такие измерения могут быть применены при градуировке тензорезисторов, а для исследования физических свойств самой пленки необходимо знать непосредственно ее деформацию (напряжения). Как известно /7/, не вся деформация передается от балки к исследуемому образцу. Передаваемая деформация зависит от размеров образца, упругих свойств образца и связующего, с помощью которого образец крепится к балке. Учет указанного эффекта может быть сделан с помощью коэффициента передачи, величина которого (для случая, когда исследуемая пленка находится в центре образца) нами была определена по формуле /8/:
Смотрите также:
ПРЕОБРАЗОВАТЕЛИ, ДАТЧИКИ, СЕНСОРЫ
Информация, новости, реклама


